Introduction
The median is an important quantity in data analysis. It represents the middle value of the data distribution. Estimates of the median, however, have a degree of uncertainty because (a) the estimates are calculated from a finite sample and (b) the data distribution of the underlying data is generally unknown. One important role of a data scientist is to quantify and to communicate the degree of uncertainty in his or her data analysis.
This time, we are going to find out what can make our sample distribution more precise during the simulation.
library(tidyverse)
library(reshape2)
Standard Normal Distribution
First, we need to set up the initial parameters. For every simulation process, we will generate 200 values base on the standard normal distribution, and we will generate them for 5000 times.
Therefore, set the sample size as 200, the test number is 5000.
sample_size <- 200
test_num <- 5000
Then let’s create a function to find out the quantile values of each test and output them as sequences.
find_quantile_value <- function(fn,sample_size, quantile_position){
sample <- fn(sample_size)
qtseq <- quantile(sample, seq(0.05,0.95,0.05))
qtseq[[quantile_position]]
}
In order to store the values of each quantile, we can create a data frame. For there are 19 quantiles and 5000 tests, the data frame should be a 5000*19 table. Then use for-loop traverse each test and each quantile.
sml_results <- as.data.frame(matrix(NA, nrow = test_num, ncol = 19))
for(i in 1:nrow(sml_results)){
for(q in 1:ncol(sml_results)){
sml_results[i,q] <- find_quantile_value(rnorm,sample_size, q)
}
}
Now we need to find the middle 95% length of the distributions of each quantile value.
length_list <- rep(NA,ncol(sml_results))
for(q in 1:ncol(sml_results)){
quantile_2.5_97.5<- quantile(sml_results[,q], c(0.025, 0.975))
length_list[q] <- quantile_2.5_97.5[[2]]-quantile_2.5_97.5[[1]]
}
Save the data we got before into a data frame and plot them.
length_df <- as.data.frame(matrix(ncol = 2, nrow = length(length_list)))
names(length_df) <- c("quantile_position","mid95_length")
length_df[,1] <- seq(0.05,0.95,0.05)
length_df[,2] <- length_list
ggplot(length_df,aes(x=quantile_position,y=mid95_length))+
geom_point()+geom_line()+
labs(title = "Length of middle 95% of normal distribution")+
scale_x_continuous(
name = "pth quantile",
breaks = seq(0.05, 0.95, 0.05)
)+
scale_y_continuous(name = "Length")

as we can see, when the quantile is approaching 50%, the length is going lower. It means that when the quantile is approaching 50%, simulation error is lower. It means when the quantile is 50%, it has the best precision.
In other words, when the quantile is 50%, the median has the tightest sampling distribution.
Then, we need to transfer the x-axis from quantile to the density values of the original distribution. In this part, it should be a standard normal distribution.
length_d_df <- length_df %>%
mutate(density=dnorm(qnorm(quantile_position)))
ggplot(length_d_df, aes(x=density,y=mid95_length))+
geom_point()+geom_line()+
labs(title = "Length of middle 95% of normal distribution by density", x= "Density",y="Length")
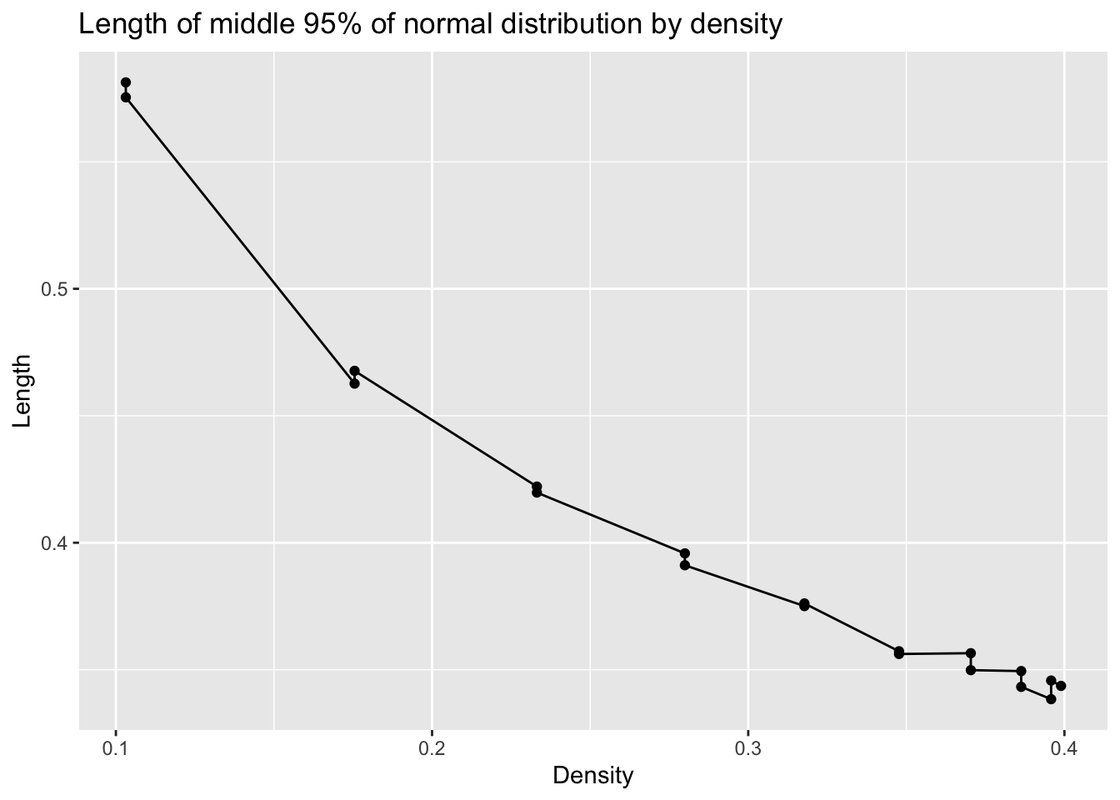
In this graph, we can find when density is bigger, the simulation error is lower.
Exponential Distribution
Distribution 2 is the exponential distribution with rate = 1.
As we did before, calculate the values of each quantile and each test then plot the graph.
for(i in 1:nrow(sml_results)){
for(q in 1:ncol(sml_results)){
sml_results[i,q] <- find_quantile_value(rexp,sample_size, q)
}
}
length_list <- rep(NA,ncol(sml_results))
for(q in 1:ncol(sml_results)){
quantile_2.5_97.5<- quantile(sml_results[,q], c(0.025, 0.975))
length_list[q] <- quantile_2.5_97.5[[2]]-quantile_2.5_97.5[[1]]
}
length_df <- as.data.frame(matrix(ncol = 2, nrow = length(length_list)))
names(length_df) <- c("quantile_position","mid95_length")
length_df[,1] <- seq(0.05,0.95,0.05)
length_df[,2] <- length_list
ggplot(length_df,aes(x=quantile_position,y=mid95_length))+
geom_point()+geom_line()+
labs(title = "Length of middle 95% of exponential distribution")+
scale_x_continuous(
name = "pth quantile",
breaks = seq(0.05, 0.95, 0.05)
)+
scale_y_continuous(name = "Length")

For this exponential distribution, when quantile is bigger, the error of simulation is bigger.
In other words, when the quantile is 5%, the median has the tightest sampling distribution.
And when the Density is higher, the error is smaller.
length_d_df <- length_df %>%
mutate(density=dexp(qexp(quantile_position)))
ggplot(length_d_df, aes(x=density,y=mid95_length))+
geom_point()+geom_line()+
labs(title = "Length of middle 95% of exponential distribution by density", x= "Density",y="Length")

Mixture Distribution 3
Distribution 3 is a mixture distribution defined by these functions.
rf3 <- function(N){
G <- sample(0:2, N, replace = TRUE, prob = c(5,3,2))
(G==0)*rnorm(N) + (G==1)*rnorm(N,4) + (G==2)*rnorm(N,-4,2)
}
pf3 <- function(x){
.5*pnorm(x) + .3*pnorm(x,4) + .2*pnorm(x,-4,2)
}
df3 <- function(x){
.5*dnorm(x) + .3*dnorm(x,4) + .2*dnorm(x,-4,2)
}
And just like we did in previous chunks, plot the middle 95% length of the quantiles.
for(i in 1:nrow(sml_results)){
for(q in 1:ncol(sml_results)){
sml_results[i,q] <- find_quantile_value(rf3,sample_size, q)
}
}
length_list <- rep(NA,ncol(sml_results))
for(q in 1:ncol(sml_results)){
quantile_2.5_97.5<- quantile(sml_results[,q], c(0.025, 0.975))
length_list[q] <- quantile_2.5_97.5[[2]]-quantile_2.5_97.5[[1]]
}
length_df <- as.data.frame(matrix(ncol = 2, nrow = length(length_list)))
names(length_df) <- c("quantile_position","mid95_length")
length_df[,1] <- seq(0.05,0.95,0.05)
length_df[,2] <- length_list
ggplot(length_df,aes(x=quantile_position,y=mid95_length))+
geom_point()+geom_line()+
labs(title = "Length of middle 95% of given mixture distribution 3")+
scale_x_continuous(
name = "pth quantile",
breaks = seq(0.05, 0.95, 0.05)
)+
scale_y_continuous(name = "Length")

Definitely, when the quantile is 40%, the median has the tightest sampling distribution.
We don’t have the qf3 function, therefore we need to use the pf3 function to calculate the values when their counterpart quantile is set. And the other part is the same as previous chunks.
pf3 <- function(x){
.5*pnorm(x) + .3*pnorm(x,4) + .2*pnorm(x,-4,2)
}
quantile_seq <- seq(0.05,0.95,0.05)
qf3_seq <- rep(NA, length(quantile_seq))
for(i in seq_along(quantile_seq)){
qf3_seq[i] <- uniroot(function(x){pf3(x)-quantile_seq[i]}, c(-100,100))[[1]]
}
length_d_df <- length_df %>%
mutate(density=df3(qf3_seq))
ggplot(length_d_df, aes(x=density,y=mid95_length))+
geom_point()+geom_line()+
labs(title = "Length of middle 95% of given mixture distribution 3 by density", x= "Density",y="Length")

Mixture Distribution 4
Mixture Distribution 4 is the following mixture distribution.
rf4 <- function(N){
G <- sample(0:1, N, replace = TRUE)
(G==0)*rbeta(N,5,1) + (G==1)*rbeta(N,1,5)
}
As previous chunks, we can plot the length of each quantile.
for(i in 1:nrow(sml_results)){
for(q in 1:ncol(sml_results)){
sml_results[i,q] <- find_quantile_value(rf4,sample_size, q)
}
}
length_list <- rep(NA,ncol(sml_results))
for(q in 1:ncol(sml_results)){
quantile_2.5_97.5<- quantile(sml_results[,q], c(0.025, 0.975))
length_list[q] <- quantile_2.5_97.5[[2]]-quantile_2.5_97.5[[1]]
}
length_df <- as.data.frame(matrix(ncol = 2, nrow = length(length_list)))
names(length_df) <- c("quantile_position","mid95_length")
length_df[,1] <- seq(0.05,0.95,0.05)
length_df[,2] <- length_list
ggplot(length_df,aes(x=quantile_position,y=mid95_length))+
geom_point()+geom_line()+
labs(title = "Length of middle 95% of given mixture distribution 4")+
scale_x_continuous(
name = "pth quantile",
breaks = seq(0.05, 0.95, 0.05)
)+
scale_y_continuous(name = "Length")

Definitely, when the quantile is 5% or 95%, the median has the tightest sampling distribution.
Base on the rf4 function we had, we can write the pf4 and df4 functions. After that, use the method we used to plot the graph.
rf4 <- function(N){
G <- sample(0:1, N, replace = TRUE)
(G==0)*rbeta(N,5,1) + (G==1)*rbeta(N,1,5)
}
pf4 <- function(x){
.5*pbeta(x,5,1) + .5*pbeta(x,1,5)
}
df4 <- function(x){
.5*dbeta(x,5,1) + .5*dbeta(x,1,5)
}
quantile_seq <- seq(0.05,0.95,0.05)
qf4_seq <- rep(NA, length(quantile_seq))
for(i in seq_along(quantile_seq)){
qf4_seq[i] <- uniroot(function(x){pf4(x)-quantile_seq[i]}, c(-100,100))[[1]]
}
length_d_df <- length_df %>%
mutate(density=df4(qf4_seq))
ggplot(length_d_df, aes(x=density,y=mid95_length))+
geom_point()+geom_line()+
labs(title = "Length of middle 95% of given mixture distribution 4 by density", x= "Density",y="Length")

Other Tests
In this part, we will focus on the situations that when sample size becomes 400, 800 and 1600.
Now use a for loop to generate all of the data given different sample sizes.
sample_size <- c(400,800,1600)
test_num <- 5000
length_df <- as.data.frame(matrix(ncol = 1+length(sample_size), nrow = length(length_list)))
names(length_df) <- c("quantile_position","400_mid95_length","800_mid95_length","1600_mid95_length")
length_df[,1] <- seq(0.05,0.95,0.05)
for(n in seq_along(sample_size)){
sml_results <- as.data.frame(matrix(NA, nrow = test_num, ncol = 19))
for(i in 1:nrow(sml_results)){
for(q in 1:ncol(sml_results)){
sml_results[i,q] <- find_quantile_value(rnorm,sample_size[n], q)
}
}
length_list <- rep(NA,ncol(sml_results))
for(q in 1:ncol(sml_results)){
quantile_2.5_97.5<- quantile(sml_results[,q], c(0.025, 0.975))
length_list[q] <- quantile_2.5_97.5[[2]]-quantile_2.5_97.5[[1]]
}
length_df[,1+n] <- length_list
}
Then plot the graph of different sample sizes and compare them.
length_df %>%
melt(id = "quantile_position") %>%
ggplot()+
geom_line(aes(x=quantile_position,y=value,color=variable))+
labs(title = "Length of middle 95% of normal distribution given different sample sizes", y = "Length")+
scale_x_continuous(
name = "pth quantile",
breaks = seq(0.05, 0.95, 0.05)
)

length_df %>%
mutate(density=dnorm(qnorm(quantile_position))) %>%
select(-quantile_position) %>%
melt(id = "density") %>%
ggplot()+
geom_line(aes(x=density,y=value,color=variable))+
labs(title = "Length of middle 95% of normal distribution given different sample sizes", y = "Length")+
scale_x_continuous(
name = "pth quantile",
breaks = seq(0.05, 0.95, 0.05)
)

Definitely, when the sample size is bigger, the error of simulation will be smaller.
In a word, when you have more simulation test, when the test number is increasing, the length will be smaller, which means the error of simulation is less than before.