Background
Roulette is a casino game named after the French word meaning little wheel. In the game, players may choose to place bets on either a single number, various groupings of numbers, the colors red or black, whether the number is odd or even, or if the numbers are high (19–36) or low (1–18). From Wikipedia-Roulette
This time we will talk about a kind of simplified Roulette, which won’t be influenced by the number on roulette but only be divided into two parts, win or lose.
To play the game successfully and avoid owing an unrealistic debt, we need to set some parameters at first. These parameters will be saved in a state list.
| Parameter | Type | Explaination |
|---|---|---|
| B | number | the budget |
| W | number | the budget threshold for successfully stoping |
| L | number | the maximum number of plays |
| M | number | the casino wager limit |
| plays | integer | the number of plays executed |
| previous_wager | number | the wager in the previous play (0 at first play) |
| previous_win | TRUE/FALSE | indicator if the previous play was a win (TRUE at first play) |
Function Setup
One Play
In order to use pipes “%>%” in code, we need to import the package first.
library(dplyr)
Then, let’s define the process of one play.
one_play <- function(state){
# Wager
proposed_wager <- ifelse(state$previous_win, 1, 2*state$previous_wager)
wager <- min(proposed_wager, state$M, state$B)
# Spin of the wheel
red <- rbinom(1,1,18/38)
# Update state
state$plays <- state$plays + 1
state$previous_wager <- wager
if(red){
# WIN
state$B <- state$B + wager
state$previous_win <- TRUE
}else{
# LOSE
state$B <- state$B - wager
state$previous_win <- FALSE
}
state
}
When the player runs out of the money or win enough money or play enough times, we need to stop the game by setting up a stop function.
stop_play <- function(state){
if(state$B <= 0) return(TRUE)
if(state$plays >= state$L) return(TRUE)
if(state$B >= state$W) return(TRUE)
FALSE
}
Multiple Plays
Next, we need to play the game under our rules as a series. The function will output a budget list to record the money value after every play.
one_series <- function(
B = 200
, W = 300
, L = 1000
, M = 100
){
# initial state
state <- list(
B = B
, W = W
, L = L
, M = M
, plays = 0
, previous_wager = 0
, previous_win = TRUE
)
# vector to store budget over series of plays
budget <- rep(NA, L)
# For loop of plays
for(i in 1:L){
new_state <- state %>% one_play
budget[i] <- new_state$B
if(new_state %>% stop_play){
return(budget[1:i])
}
state <- new_state
}
budget
}
Then we can get the final result of this series of play.
# helper function
get_last <- function(x) x[length(x)]
get_series <- function(x) x
Simulation
In order to figure out the generalized result, we need to repeat the process for a huge number of times then try to find out the distribution and other characteristics of results.
# Simulation
walk_out_money <- rep(NA, 1000)
for(j in seq_along(walk_out_money)){
walk_out_money[j] <- one_series(B = 200, W = 300, L = 1000, M = 100) %>% get_last
}
# Walk out money distribution
hist(walk_out_money, breaks = 100)
# Estimated probability of walking out with extra cash
mean(walk_out_money > 200)
# Estimated earnings
mean(walk_out_money - 200)
Compare
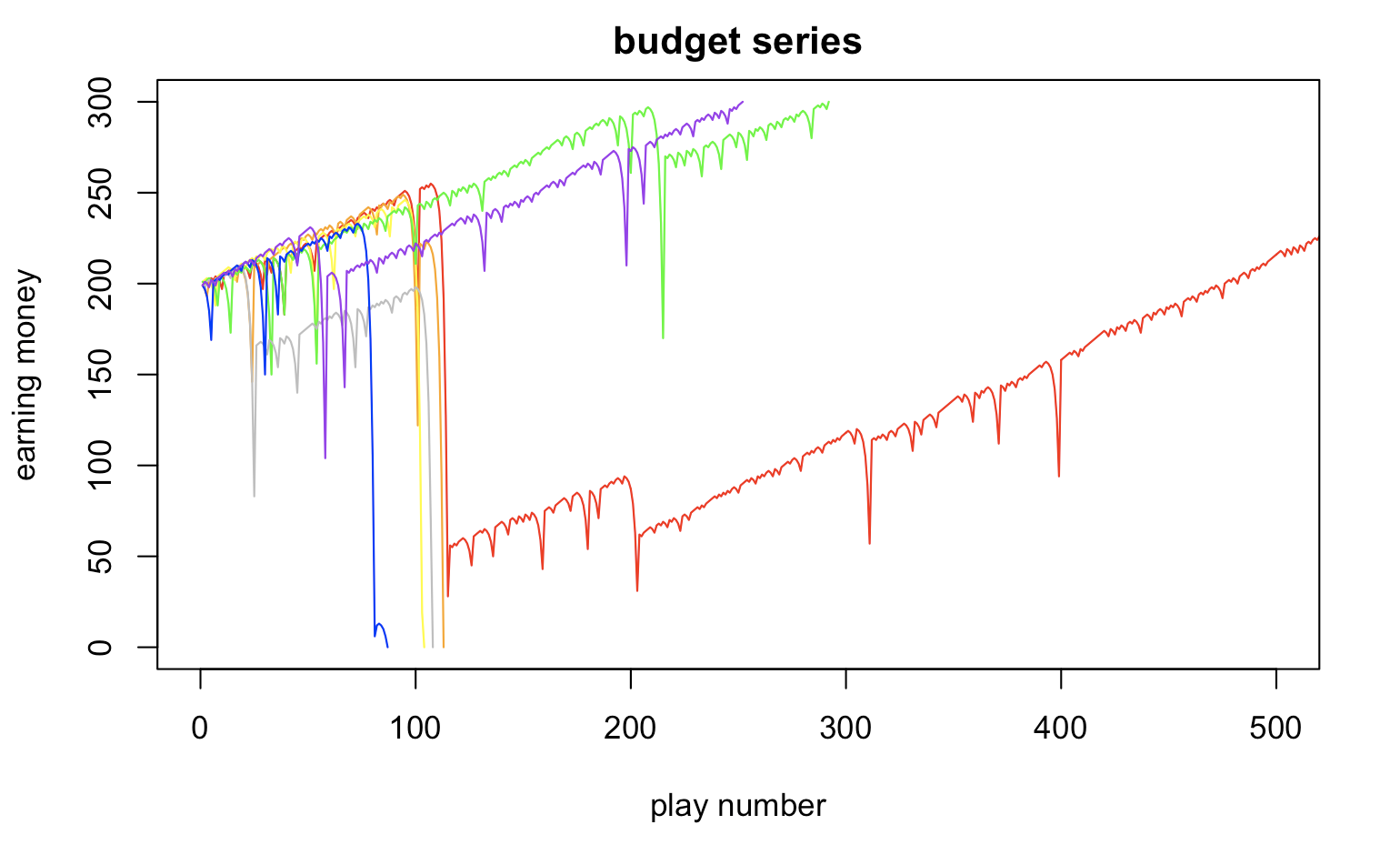
In this graph, we can see how the budget changes during one series.
budget_list <- one_series(B = 200, W = 300, L = 1000, M = 100) %>% get_series
plot(budget_list, type="l", xlim=c(0,500), ylim=c(0,300), xlab="play number", ylab="earning money", main="budget series",col="red")
budget_list <- one_series(B = 200, W = 300, L = 1000, M = 100) %>% get_series
lines(budget_list, col="orange")
budget_list <- one_series(B = 200, W = 300, L = 1000, M = 100) %>% get_series
lines(budget_list, col="yellow")
budget_list <- one_series(B = 200, W = 300, L = 1000, M = 100) %>% get_series
lines(budget_list, col="green")
budget_list <- one_series(B = 200, W = 300, L = 1000, M = 100) %>% get_series
lines(budget_list, col="gray")
budget_list <- one_series(B = 200, W = 300, L = 1000, M = 100) %>% get_series
lines(budget_list, col="blue")
budget_list <- one_series(B = 200, W = 300, L = 1000, M = 100) %>% get_series
lines(budget_list, col="purple")
| Parameter | Type | Explaination |
|---|---|---|
| B | number | the budget |
| W | number | the budget threshold for successfully stoping |
| L | number | the maximum number of plays |
| M | number | the casino wager limit |
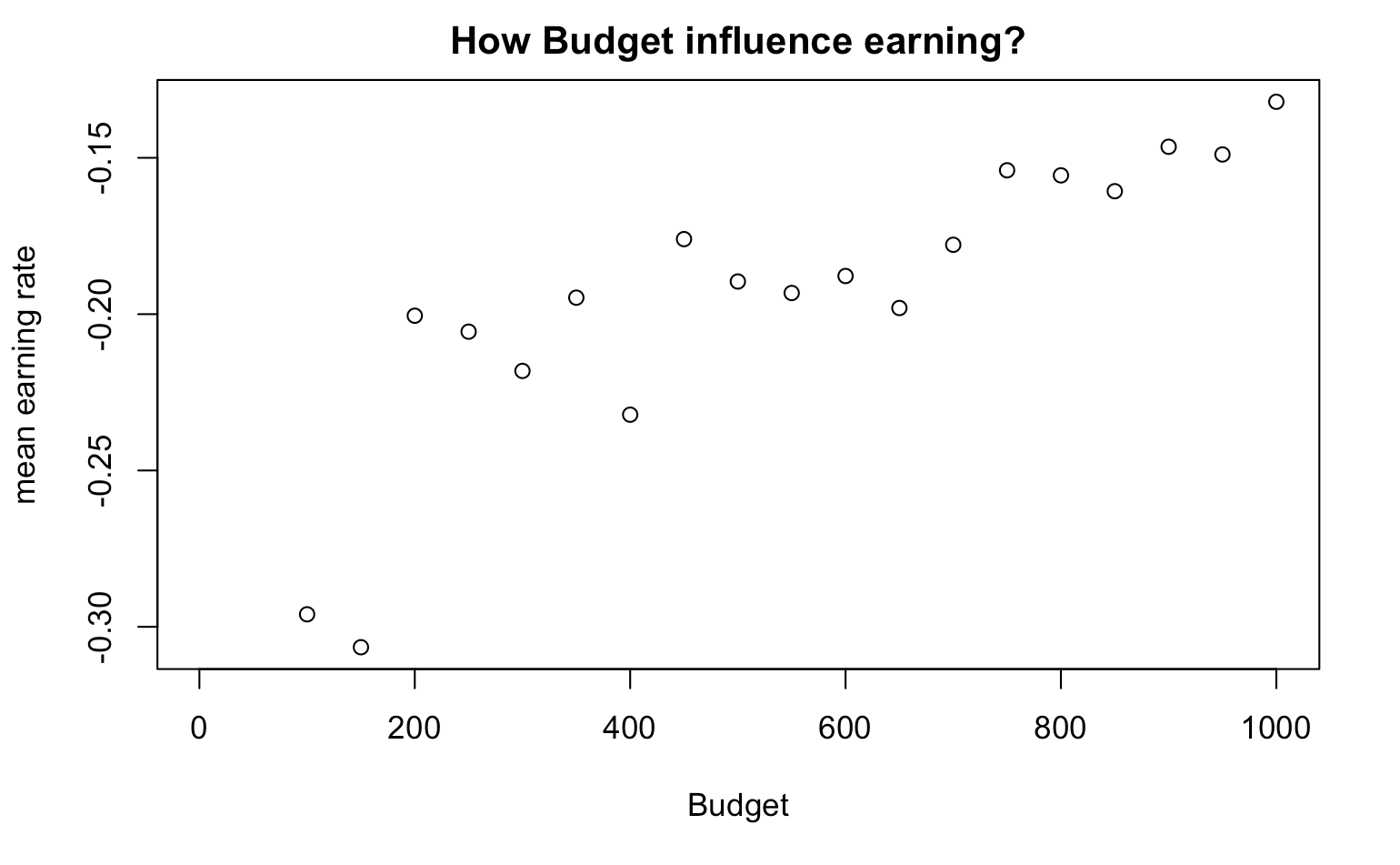
Change the budget
When B changes, what is the mean earning?
earning_series <- rep(NA,20)
for(B in seq(100,1000,by=50)){
walk_out_money <- rep(NA, 1000)
for(j in seq_along(walk_out_money)){
walk_out_money[j] <- one_series(B, W=B+100, L = 1000, M = 100) %>% get_last
}
earning_series[B] <- mean(walk_out_money - B)/B
}
plot(earning_series,xlab="Budget",ylab="mean earning rate", main="How Budget influence earning?")
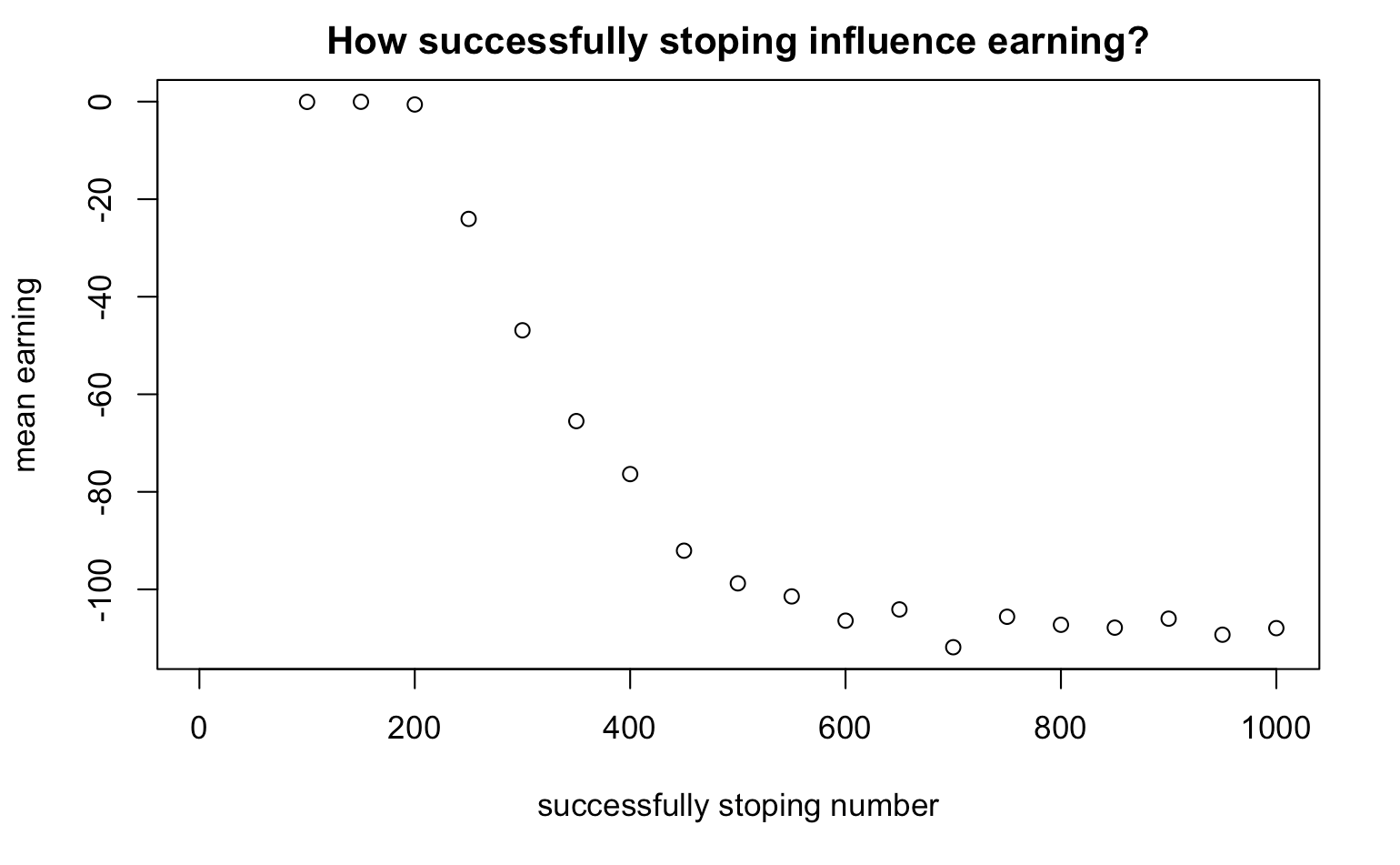
Change the budget threshold for successfully stoping
When W changes, what is the mean earning?
earning_series <- rep(NA,20)
for(W in seq(100,1000,by=50)){
walk_out_money <- rep(NA, 10000)
for(j in seq_along(walk_out_money)){
walk_out_money[j] <- one_series(B=200, W, L = 1000, M = 100) %>% get_last
}
earning_series[W] <- mean(walk_out_money - 200)
}
plot(earning_series,xlab="successfully stoping number",ylab="mean earning", main="How successfully stoping influence earning?")
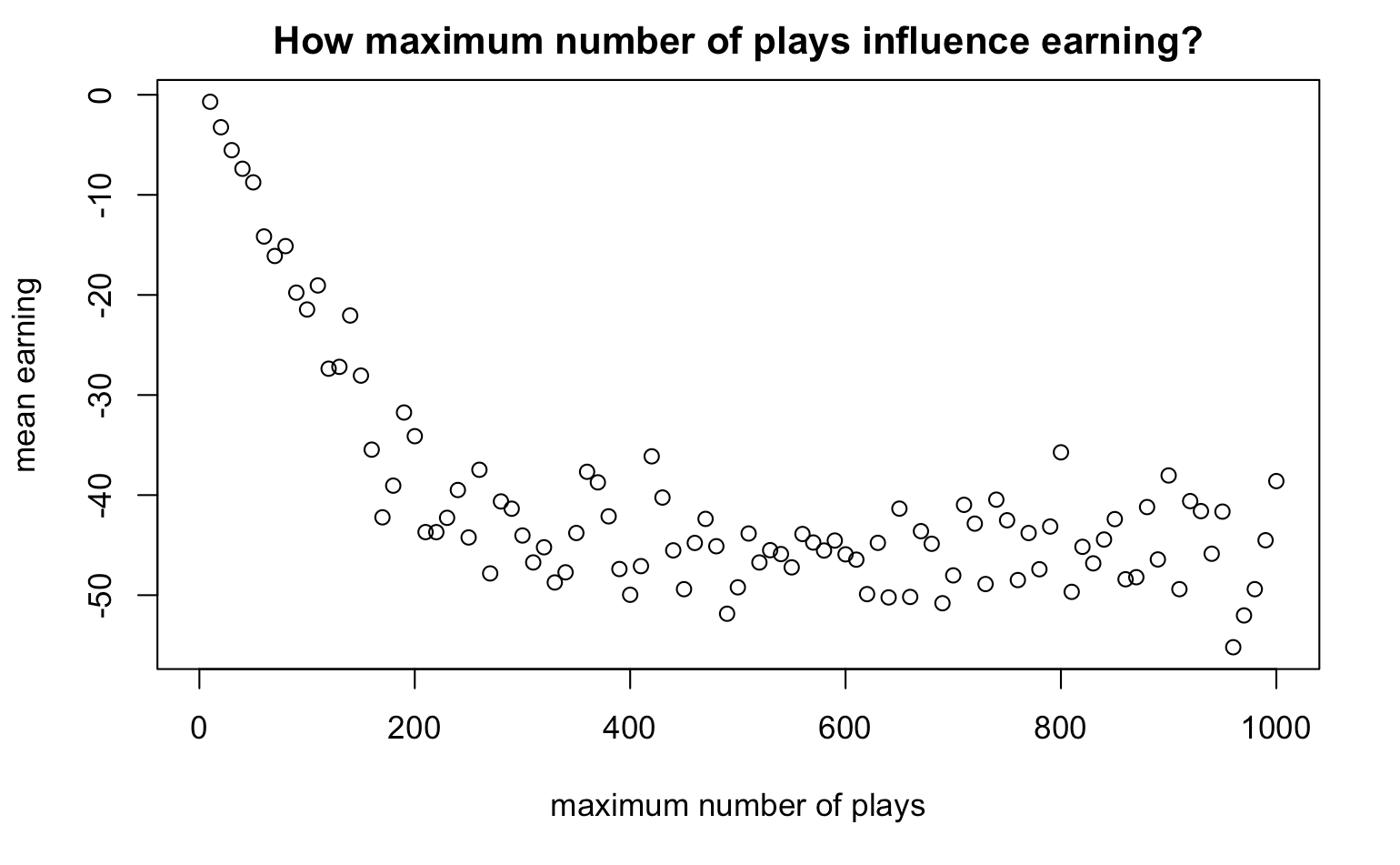
Change the maximum number of plays
When L changes, what is the mean earning?
earning_series <- rep(NA,100)
for(L in seq(10,1000,by=10)){
walk_out_money <- rep(NA, 1000)
for(j in seq_along(walk_out_money)){
walk_out_money[j] <- one_series(B=200, W=300, L, M = 100) %>% get_last
}
earning_series[L] <- mean(walk_out_money - 200)
}
plot(earning_series,xlab="maximum number of plays",ylab="mean earning", main="How maximum number of plays influence earning?")
Change the casino wager limit
When M changes, what is the mean earning?
earning_series <- rep(NA,100)
for(M in seq(10,1000,by=10)){
walk_out_money <- rep(NA, 1000)
for(j in seq_along(walk_out_money)){
walk_out_money[j] <- one_series(B=200, W=300, L=500, M) %>% get_last
}
earning_series[M] <- mean(walk_out_money - 200)
}
plot(earning_series,xlab="casino wager limit",ylab="mean earning", main="How casino wager limit influence earning?")
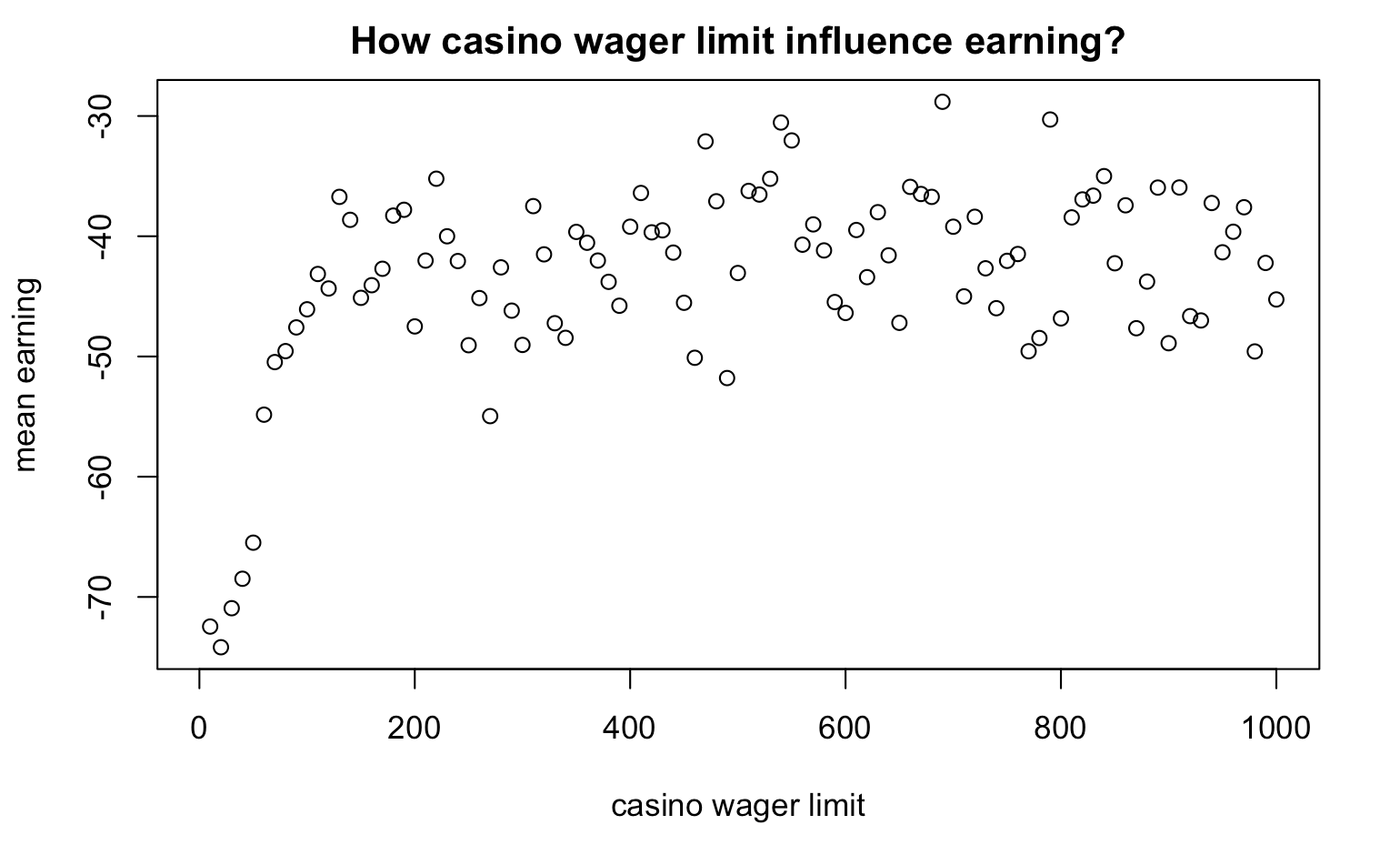
Play times
Next, we can save the times that the game played before walkout then find out the characteristics.
get_times <- function(x) length(x)
walk_out_times <- rep(NA, 10000)
for(j in seq_along(walk_out_times)){
walk_out_times[j] <- one_series(B = 200, W = 300, L = 1000, M = 100) %>% get_times
}
hist(walk_out_times, breaks = 100)
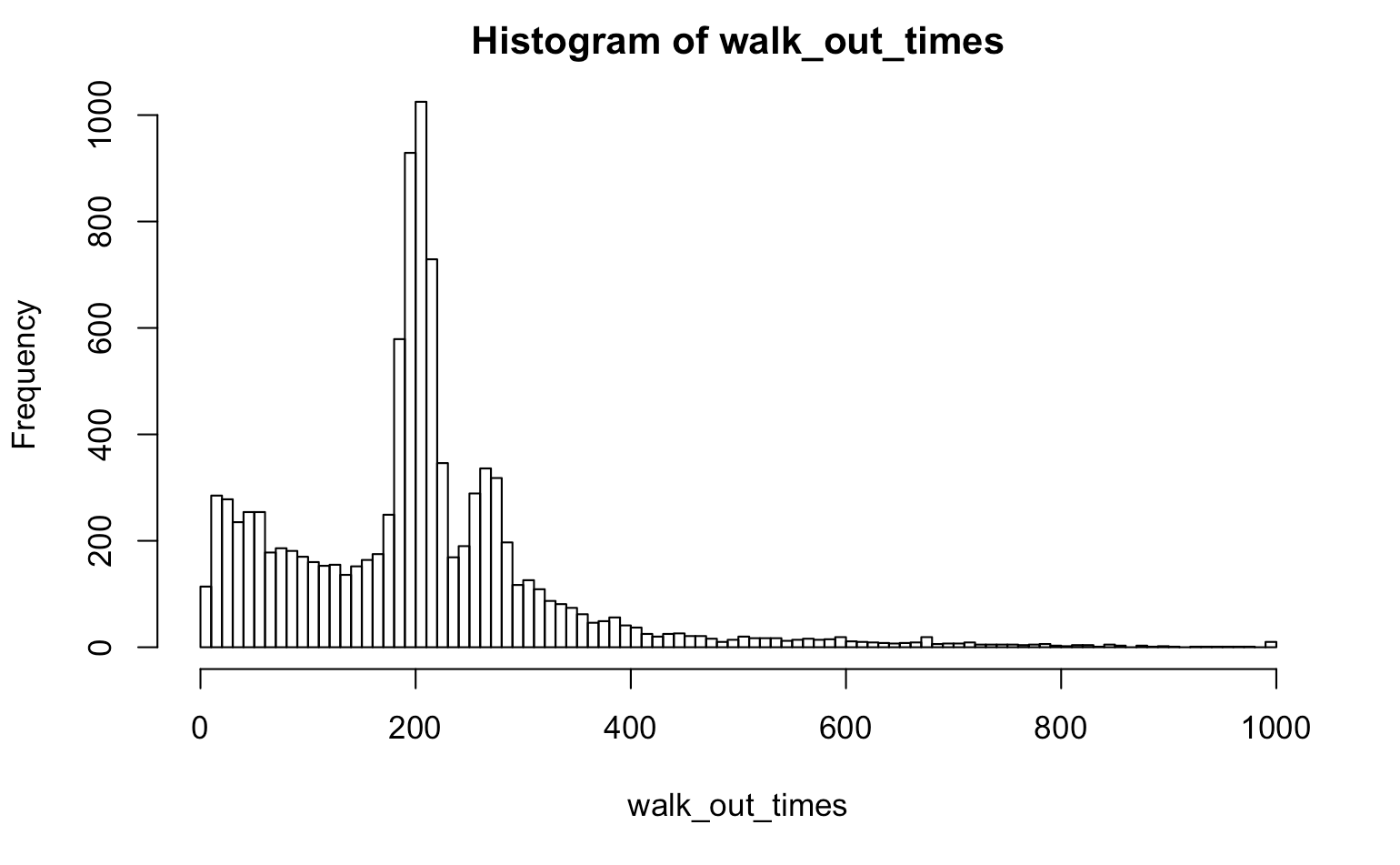
mean(walk_out_times)
The mean of walk out time is 203.0846.
The limitation of simulation is obvious. It is a black box actually. We can not use it as we proof it by mathematical method. We don’t know why it happened and how it happened, so we can only change the parameter to try to understand the process. By the way, it is not a precise result. Every time we get an answer, it will change a little bit next time.