Import the package at the very first.
library(tidyverse)
Introduction

The World Series is the annual championship series of Major League Baseball (MLB) in North America, contested since 1903 between the American League (AL) champion team and the National League (NL) champion team. The winner of the World Series championship is determined through a best-of-seven playoff, and the winning team is awarded the Commissioner’s Trophy. As the series is played during the fall season in North America, it is sometimes referred to as the Fall Classic.
From Wikipedia - World Series
In this blog, we are going to calculate the probability of several questions about the Braves and the Yankees in the World Series.
First, we need to define some parameters.
| Parameter | Explaination |
|---|---|
| PB | In any given game, the probability that the Braves win |
| PY = 1 - PB | in any given game, the probability that the Yankees win |
Questions
1. What is the probability that the Braves win the World Series given that PB=0.55?
First,we need to set the value of PB and PY.
PB <- 0.55
PY <- 1- PB
Create a function to calculate the probability of a win. The win is defined as win 4 times in 7 games.
calc_prob <- function(p){
pnbinom(3, 4, p)
}
Now calculate the probability given that PB=0.55.
calc_prob(PB)
Obviously, when the PB is 0.55, the probability that Braves win the World Series is 0.608.
2. What is the probability that the Braves win the World Series given that PB=x?
Now the PB is not defined yet, so we should assume the x could be any number between 0.5 to 1.
First, we need to generate a series of PB and the probability results.
PBseries <- seq(0.5, 1, 0.01)
win_prob <- rep(NA, length(PBseries))
Now use the function we used before to calculate the probability given every PB.
for(i in 1:length(win_prob)){
win_prob[i] <- calc_prob(PBseries[i])
}
In order to interpret the relationship between PB and the probability that the Braves win, we can draw a graph for them.
plot(x = PBseries,
y = win_prob,
xlim = c(0.5,1),
ylim = 0:1,
xlab = "Probability of the Braves winning a head-to-head matchup",
ylab = "P(Braves win World Series)",
main = "Probability of winning the World Series")
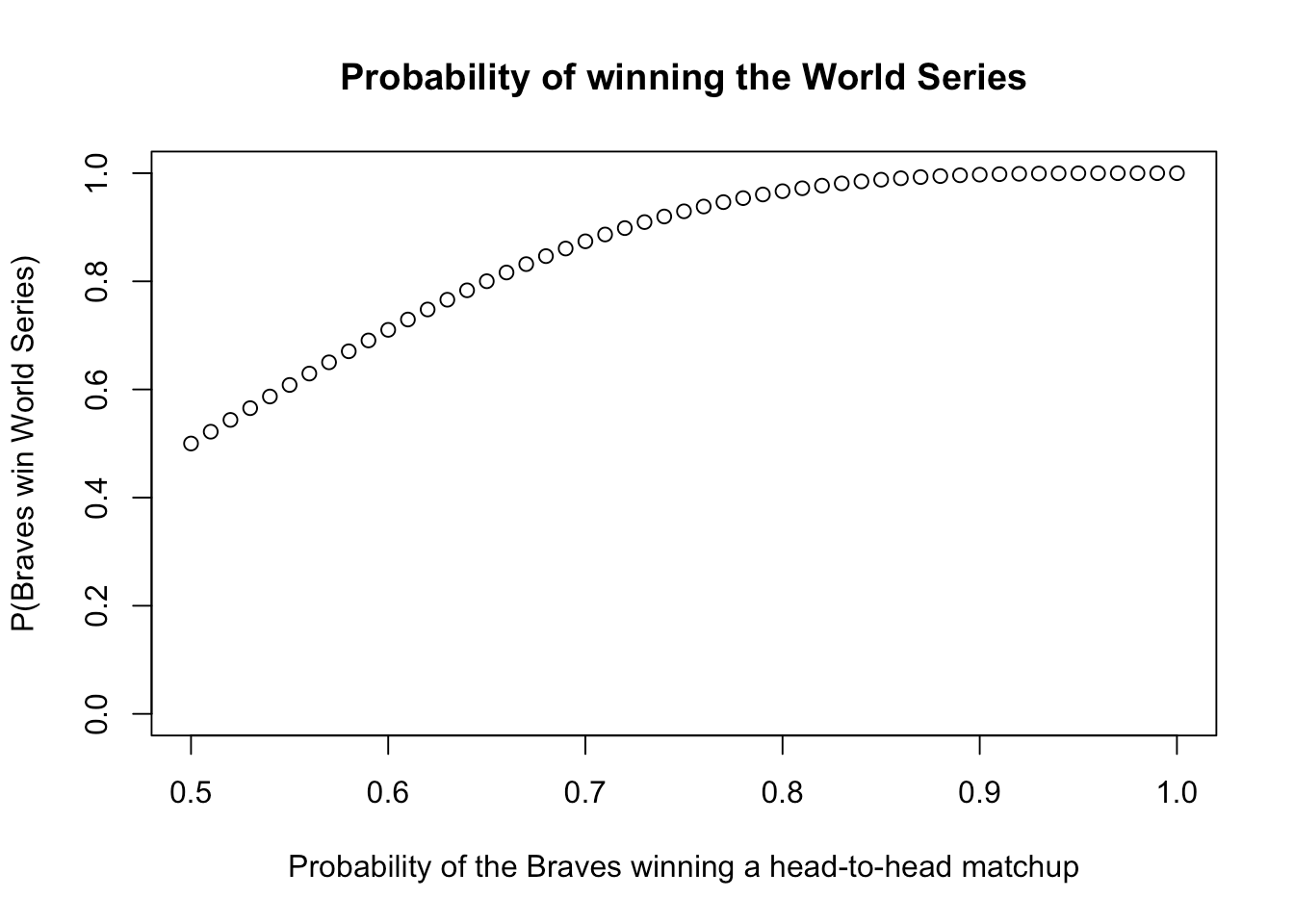
As we can see, in this graph, when PB is increasing, the probability that the Braves win the World Series is increasing too. In fact, when we change the x scale to 0.0-1.0, we will find the line looks like a logistic curve.
3. Suppose one could change the World Series to be best-of-9 or some other best-of-X series. What is the shortest series length so that P(Braves win World Series|PB=0.55) ≥ 0.8?
As same as the first question, the PB needs to be 0.55. And now the game series length is not certain. Definitely, the series length should be an odd number.
PB <- 0.55
series_length <- seq(1, 999, 2)
Now we need to create a function to calculate the probability when the series length is a parameter.
calc_prob_sl <- function(sl){
win_threshhold <- ceiling(sl/2)
pnbinom(win_threshhold - 1, win_threshhold, 0.55)
}
In the end, given every series length, calculate the probability that the Braves win World Series. When the probability is equal to or more than 0.8, stop running and give the series length value and the probability.
for(i in 1:length(series_length)){
pb_win <- calc_prob_sl(series_length[i])
if(pb_win >= 0.8){
shortest <- series_length[i]
p_shortest <- pb_win
break}
}
shortest
p_shortest
Now we get the shortest series length. It should be 71. In that situation, the probability that the Braves win World Series is about 0.802.
4. What is the shortest series length so that P(Braves win World Series|PB= x) ≥ 0.8? This will be a figure (see below) with PB on the x-axis and series length is the y-axis.
Now the PB has not defined again, so we should assume the x could be any number between 0.51 to 1.
First, we need to generate a series of PB and a series to save the length results given different PB. But the way, we also need a series of the possible series length we will test. Now the ceiling is 9999. If it’s not enough, we can set a bigger limitation.
PBseries <- seq(0.51, 1, 0.01)
length_record <- rep(NA, length(PBseries))
series_length <- seq(1, 9999, 2)
In order to calculate the probability that the Braves win the WS, we need a new function with 2 input, because both of the series length and PB are variables.
calc_prob_sl_p <- function(sl,pb){
win_threshhold <- ceiling(sl/2)
pnbinom(win_threshhold - 1, win_threshhold, pb)
}
Now, calculate the shortest series length when PB is changing. Save the values in length_record.
for(j in 1:length(PBseries)){
for(i in 1:length(series_length)){
pb_win <- calc_prob_sl_p(series_length[i],PBseries[j])
if(pb_win >= 0.8){
shortest <- series_length[i]
break}
}
length_record[j] <- shortest
}
We have already got the shortest series length given different PB. Let’s draw the figure to show the relationship between them.
plot(x = PBseries,
y = length_record,
xlim = c(0.5,1),
xlab = "Probability of the Braves winning a head-to-head matchup",
ylab = "Series length",
main = "Shortest series so that P(Win WS given p)>=0.8")
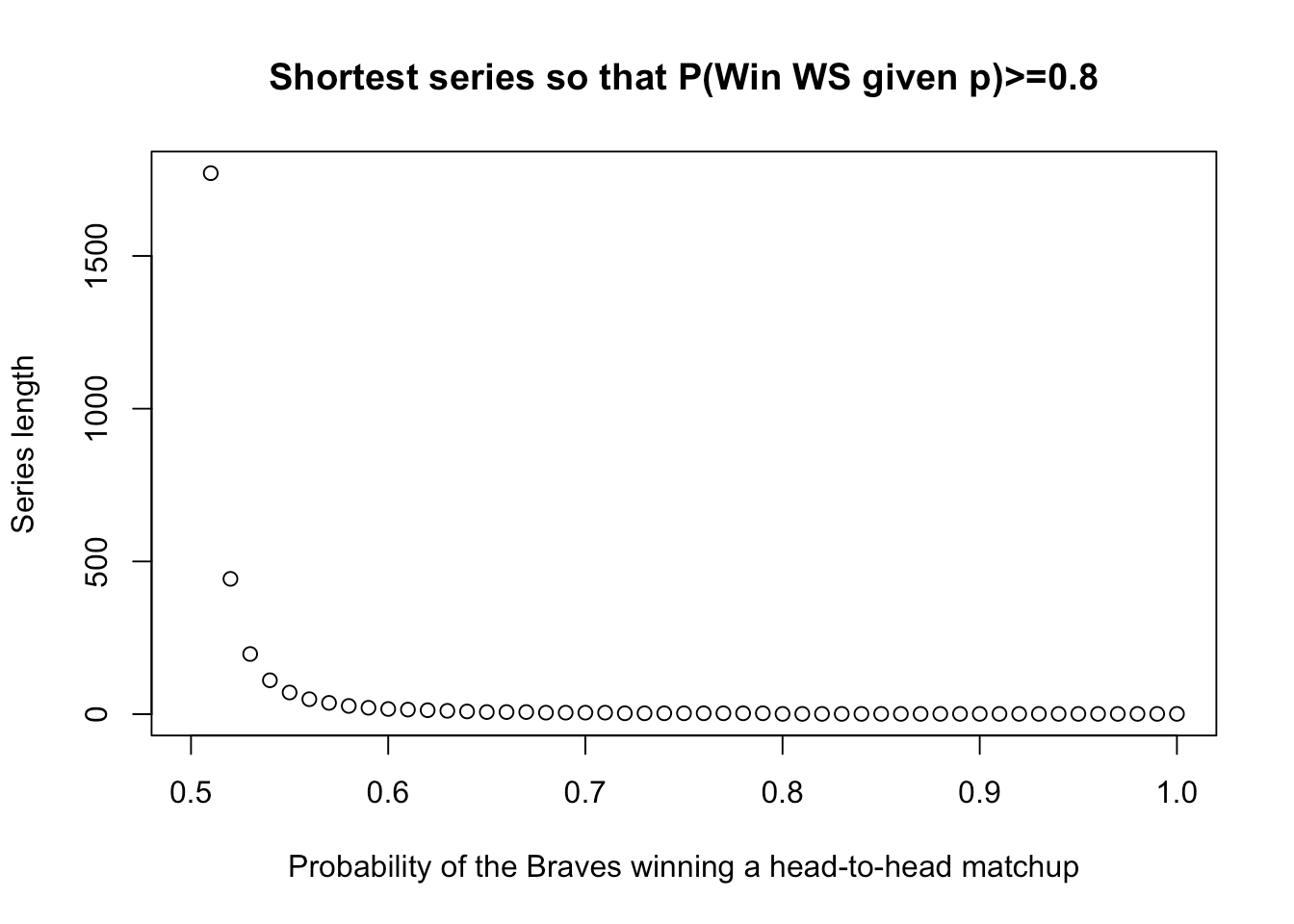
in this graph, when PB is increasing, the shortest series length, when the probability that the Braves win the World Series is more than 0.8, is approaching 1. When the PB is bigger than 0.8, the shortest series length is 1.
5. Calculate P( PB=0.55|Braves lose 3 games before winning a 4th game) under the assumption that either PB=0.55 or PB=0.45. Explain your solution.
According to Conditional probability formula, we can get:
\[P(A|B)=\frac{P(A)P(B)}{P(B)} \to P(A)P(B)=P(A|B)P(B)\\ P(B|A)=\frac{P(A)P(B)}{P(A)} \to P(A)P(B)=P(B|A)P(A)\\ \to P(A|B)P(B)=P(A)P(B)=P(B|A)P(A)\\ \to P(A|B)=\frac{P(B|A)P(A)}{P(B)}\]Now the P(A) = P(PB=0.55), P(B) = P(Braves lose 3 games before winning a 4th game). As a result, P( PB=0.55|Braves lose 3 games before winning a 4th game) = P(Braves lose 3 games before winning a 4th game|PB=0.55) * P(PB=0.55) ÷ P(Braves lose 3 games before winning a 4th game).
P(PB=0.55) = 0.5
Then use dnbinom() calculate P(Braves lose 3 games before winning a 4th game) and P(Braves lose 3 games before winning a 4th game|PB=0.55):
(dnbinom(3,4,0.45)+dnbinom(3,4,0.55))/2
dnbinom(3,4,0.55)
P(Braves lose 3 games before winning a 4th game) = 0.1516092
P(Braves lose 3 games before winning a 4th game | PB=0.55) = 0.1667701
P( PB=0.55|Braves lose 3 games before winning a 4th game) = P(Braves lose 3 games before winning a 4th game|PB=0.55) * P(PB=0.55) ÷ P(Braves lose 3 games before winning a 4th game)
0.1667701 * 0.5 / 0.1516092
P( PB=0.55|Braves lose 3 games before winning a 4th game) = 0.1667701 * 0.5 ÷ 0.1516092 = 0.5499999
Therefore, P( PB=0.55|Braves lose 3 games before winning a 4th game) is 0.5499999, about 0.55.